“熵理论,对于整个科学来说是第一法则。”
——爱因斯坦
这是科幻小说《三体》中,关于超高级文明生物“歌者”的一段描述。“歌者”将人类以及三体文明等其他文明称为“低熵体”,生命若要维持,就要想方设法将自己的熵降低,走向有序。
这个设定的确有根有据,薛定谔振聋发聩的论述——“生命以负熵为生,人活着的意义,就是不断对抗熵增的过程”,便说明了这个道理。

图 薛定谔 图源| 维基百科
而诺贝尔物理学奖获得者彭罗斯曾在名为《The Road to Reality》的书中提出这样的观点:“太阳给地球提供‘低的熵’,人类生活以及大自然消耗低熵能量后再回馈给太阳‘高的熵’。” 既然熵总是趋于最大值,那么人类的生老病死就是一个自然规律,是走向熵增的道路。
“熵”,已然横跨多个领域,成为科普作品、文艺作品甚至是心灵鸡汤的高频词。在科学研究中,起源于物理学的“熵”在许多领域都有着广泛的应用。今天,我们主要从微观层次聊聊熵理论和物理学的那些事儿。
1 什么是熵?
1865年,德国物理学家克劳修斯首次提出熵的概念,用来表示任何一种能量在空间中分布的均匀程度,能量分布得越均匀,熵就越大。我们可以理解为,熵是表示物质系统状态的一种度量:熵越大,系统越无序;熵越小,系统越有序。
随后,熵被用来进行热力学和统计学意义上的解释。1948年,贝尔实验室的香农提出了“信息熵”,解决了对信息的量化度量问题。香农认为,信息是人们对事物了解的不确定性的消除或减少,他把通讯过程中信源讯号的平均信息量称为信息熵(现在也被称为香农熵)。

图 克劳德·香农(Claude Elwood Shannon)图源| bbvaopenmind
拿扑克牌来说,一副扑克牌有五十四张牌,就具有五十四张牌的信息,抽牌过程就是获取信息的过程。最开始,我们对下一张牌的信息一无所知,信息为零,信息熵最大。随着不断抽牌,信息熵逐渐减小。最后只剩一张牌的时候,看看手里的五十三张牌,就可以确定最后一张牌的信息了,此时信息熵为零。这就是信息熵在传递信息过程中的变化形式。

图 扑克牌的抽取过程就是获取信息的过程 图源| pixabay
现在,信息熵的研究得到了不断发展,由香农信息熵演化出来了多种信息熵分析方法,比如:联合熵、条件熵、相对熵、交叉熵和互信息熵等。
2 最大熵原理
香农提出的信息熵的概念能很好地量化度量信息,却忽略了一个问题:从理论上讲,对于给定的随机变量,如何获取最为合适的一个分布呢? 美国物理学家杰恩斯提出的最大熵原理回答了这个问题。

图 杰恩斯 (Edwin Thompson Jaynes) 图源| bayes.wustl.edu
1957年,杰恩斯根据最大熵原理推导出的概率分布重新表述了统计力学。这种理论的重新表述简化了数学,允许理论的基本扩展,并将统计力学重新解释为基于不完整信息的推理。
熵作为一个非常重要的物理量,已广泛应用于热力学、信息论、统计物理学、生物学、经济学等许多领域。下面,我们将介绍熵在核物理学中的一些应用。
3 信息熵和核物理学
我们可以将核子和原子核视为通过强相互作用紧密结合起来的多体复杂系统。利用香农信息熵和最大熵原理,科学家们也可以探索在费米尺度下多体系统中的特殊的结构和行为。我们以时间为序举几个例子,介绍熵在核物理研究中的一些应用。
图 核物理学是研究在极小的费米尺度下的组成部分以及他们之间的相互作用的重要物理学领域。图源| Jefferson Lab
1995至1996年间,曹臻和华家照教授利用信息熵研究了分支过程中粒子的产生。他们研究了量子电动力学和量子色动力学过程的信息熵。这里,和信息熵密切相关的一个物理量是Koba-Nielsen-Olesen (KNO)标度律,它在理解强子行为方面发挥了重要作用。
信息熵理论还可以为理解重离子碰撞过程中的物理现象提供新的方法和观测资料。1999年,马余刚院士首次提出在重离子碰撞及其碎片产生中可以观察到齐普夫定律(该定律最早是语言学等领域的经验观察,即词的出现频率与其等级成反比)。这一想法不久在欧洲核子中心的实验和在美国的实验中得到了应用和验证。基于信息熵的混沌性分析反映了碰撞系统的有序性,可以作为核物质演化的指标,为重离子物理学开辟了新的思路。

图 乔治·金斯利·齐普夫(George Kingsley Zipf)图源| gf.org
2015年,中科院近代物理所研究团队把最大熵原理应用到强子结构研究中,把熵和强子内部的夸克动量分布联系起来,获得了质子、π和K介子内部价夸克在低能标下的动量分布。最大熵方法作为一种新的方法,可以比较简洁地给出结果,并且和实验测量符合得很好。
4 质子世界中的纠缠熵
上面,我们讨论的是经典的信息熵概念,而在量子层面,科学家们用“纠缠熵”来描述对事件的“无知”程度。
热力学熵描述的是“粗粒化”带来的“无知”,也就是只假设知道一些宏观的热力学量,而对微观状态一无所知。在量子层面,信息就不能用经典的热力学熵了,很显然,信息载体变成了一个又一个的概率,变得十分抽象。将经典的信息熵推广到量子层面,是冯·诺依曼的经典工作之一,被称为纠缠熵(也被称为冯·诺伊曼熵)。

图 冯·诺依曼(John von Neumann) 图源| 维基百科
那么,和“纠缠”到底有啥关系呢?爱因斯坦起初将量子力学中的超距作用称作“幽灵”,他不相信有超光速的作用存在。举个例子:
假如你把一副手套左右各一只分别放进两个箱子里,跋山涉水将其中一个放到海王星上,另一个就放家里。你让你的好朋友去海王星打开那个箱子,他打开的一瞬间就知道你家里那只是左手的还是右手的。这个信息量是一瞬间的传递,多远都可以。这明显超光速了啊!
爱因斯坦联合他的两个小伙伴波多尔斯基和罗森写了文章坚决抵制这个“幽灵”,后世称作“爱因斯坦-波多尔斯基-罗森佯谬”。不过,此后很多实验都验证了超距作用的存在(2022年颁发的诺贝尔物理学奖与此相关)。这种超距作用的实质是量子纠缠,可由量子纠缠熵来描述。
01① 黑洞辐射过程与佩奇曲线
纠缠熵被应用来研究黑洞辐射过程。黑洞一般被认为是连光都能吸收的天体,任何东西都不能从黑洞逃逸出来。1973年,霍金预言黑洞会产生黑体辐射,称为“霍金辐射”。霍金辐射说明黑洞会释放出信息(热辐射),这一行为导致信息不守恒了,此即“黑洞信息佯谬”。
1993 年,霍金的学生佩奇(当然不是小猪乔治的姐姐)计算了黑洞的纠缠熵,曲线像一个倒V字,这就是著名的“佩奇曲线”。佩奇曲线成功地描述了黑洞辐射过程的纠缠熵变化。
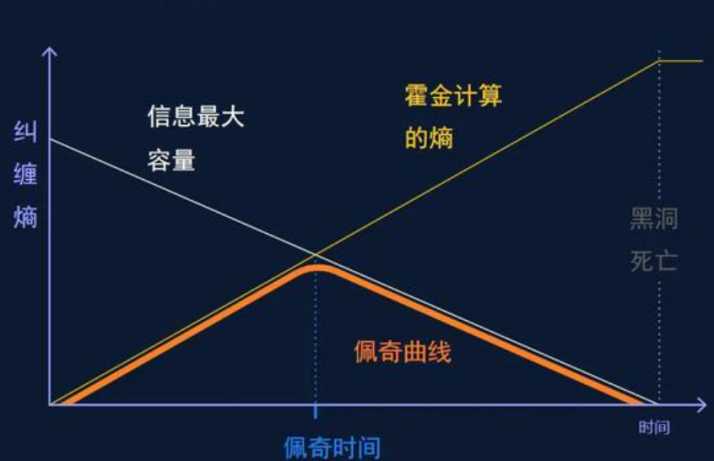
图 佩奇曲线。当黑洞释放辐射时,黑洞和辐射在量子力学上是有联系的,联系的总量叫纠缠熵。根据霍金的计算,熵会一直增长到黑洞死亡。但是如果信息从黑洞中逃逸,纠缠熵就应遵循佩奇曲线。图源| Samuel Velasco/Quanta Magazine
② 质子内部的纠缠熵
佩奇曲线是直接从量子系统出发的,因此原则上可以应用到任意量子系统中。近年来,科学家们发现,纠缠熵也能应用于微观世界的质子结构研究,这提供了一个崭新的研究思路。
质子作为一个纯态量子系统,人们曾普遍认为其是零纠缠的。但实际上,深层次的质子结构是复杂的,除了三种价夸克之外,还有一堆从真空涨落出来的胶子夸克海,这些统称为“部分子”。电子-质子深度非弹性散射实验可以用以研究质子的深层次内部结构。大量的实验表明,是量子纠缠将质子内部这些粒子彼此联系起来。

图 质子包含称为夸克和胶子的较小粒子。实验数据表明,量子纠缠将这些粒子彼此联系起来。图源| sciencenews.org
质子在深度非弹性散射实验中恰好可以根据光子探测区域与未知区域分成两个子系统。2022年,中科院近代物理所研究团队提出:应该用著名的“佩奇纠缠公式”来计算两个子系统之间的纠缠熵。
质子内部应该是最大的量子纠缠:一个进入质子内部的光子看到的那部分,必须以这种最大的方式与看不见的那部分纠缠在一起。因此,我们可以推断出:电子-质子深度非弹性散射过程的末态强子多重数分布应该对应最大纠缠熵。这个推断已经被实验证实了。
从而,黑洞和高能核物理两个研究领域通过熵的概念建立了新的联系,为理论进步和实验研究提供了新的途径。
5 理解宇宙奥秘的桥梁
熵原本是分子热力学的一个概念,现在被广泛应用于物理、化学、生物、信息科学等自然科学以及工程技术的许多领域。如今,人们对熵理论的认识仍然在不断深入,已经深入到物质最微观的层次和黑洞,甚至深入到时空的研究了。
熵与最微观层次之间的联系表明,不同学科的多个系统中的模式和结构可能具有共同的原则,熵是对大自然的一种基本描述。这种扩展的理解可以帮助指导研究人员加深对原子核结构和它们的相互作用以及它们在更广泛的科学背景中的作用的理解。
熵的研究,处于当今众多学科研究工作的前沿,必将进一步促进我们对自然界的进一步理解,是人类理解宇宙奥秘的一座桥梁!
致谢:感谢马春旺教授阅读本文并提出宝贵建议。
作者| 寇维 陈旭荣
封面图来源| James LaPlante/Sputnik Animation
#参考文献:
1. E. T. Jaynes, Phys. Rev. 106 620 (1957).
2. Y. G. Ma, Phys. Rev. Lett. 83 (1999) 3617.
3. C. W. Ma, Y. G. Ma, Prog. Part. Nucl. Phys. 99, 120–158 (2018).
4. R. Wang and X. Chen, Phys Rev D 91 (2015) 054026.
5. W. Kou, X. Wang, X. Chen. Phys. Rev. D 106.096027 (2022).
转载内容仅代表作者观点
不代表中科院物理所立场
如需转载请联系原公众号
来源:中科院近代物理所
编辑:见欢
































